مُلخَّص خوارزميّة المُحوِّل

خوارزمية المُحوّل هي إحدي الخوارزميات الأكثر فعالية ورواجا في هذه الفترة. وقد صيغ هذا الاسم ونُشر تصميمُ هذه الخوارزمية بادِئ الأمر سنة 2017 في الورقة البحثيّة المشهورة “الانتباه هو كُلُّ ما تحتاجه”[1]. فماهي طريقة عملها ومالذي يُميّزها؟
صُمِّمت خوارزمية المُحوّل لحلّ مشاكل التعلُّم على تسلسُلات البيانات، ودرج أهل الإختصاص على تسمية هذا النوع من البيانات ب”التسلسُلات” اِختصارًا. وهي تندرج في صنف التعلُّم من التسلسُل إلى التسلسُل، ونقصد بذلك النماذج وطُرق التعلُّم التي تُمكِّن من تعليم نموذجٍ ما كيفَ يُحوِّلُ سلسلةً مُدخلة ما إلى سلسلةٍ أخرى مُقابِلة لها لتنفيذ مهمَّة من مهمّات مُعالجة اللّغة الطبيعية كالترجمة من لُغة إلى أخرى. مثلا، قد تكونُ السلسلة المُدخلة جُملةً باللغة الإنجليزية، والسلسلةُ المُخرجة ترجمةَ تلك الجُملة إلى اللُغة العربية. أو قد تكون السلسلة المُدخلة مقطعًا صوتيا والسلسلة المُخرجة الجُملةَ النصيَّة المُوافقة لما في المقطع الصوتي. وفي العموم، المقصود بالتسلسُل: أيُّ بياناتٍ مُدخلة تتكون من رموز متوالية تؤدّي معنى معًا، ومنها الجُمل والأصوات والفيديوهات، … إلخ.
كغيرها من خوارزميات التعلُّم على التسلسُلات التي انتشرت منذ سنة 2014، صُممت خوارزمية المُحوِّل اعتمادًا على هيكلة تتكوّن من جُزئين: الترميز + فكّ الترميز. وقُدِّم هذا التصميم في الورقة البحثيّة “التعلُّم من التسلسُل إلى التسلسُل باستعمال الشبكات العصبية”[2] حيثُ أدَّى إلى تحسينِ أداء التعلُّم الآلي بشكل ملحوظ على مهمَّة الترجمة الآلية من الإنجليزيّة إلى الفرنسيّة، ممّا أدّى إلي انتشار استعمالها في مجتمع البحث العلمي.
يتكامَلُ جُزءا مِعمارية المُحوّل لمُعالجة التسلسُل المُدخل بهدف إنشاء التسلسُل المُخرج كما هو مُبيّن في الرسم التوضيحي التّالي.
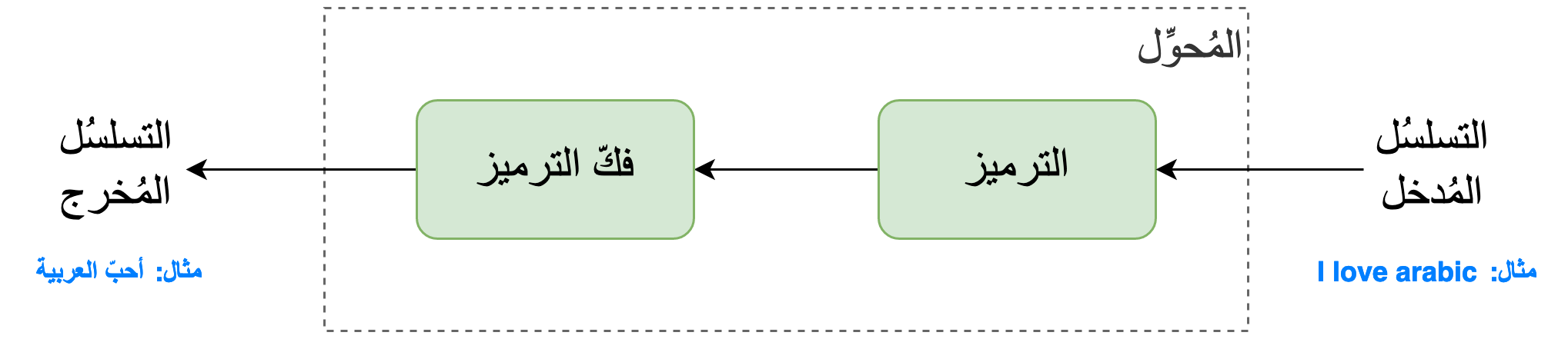
يقومُ جُزءُ التّرميز بمُعالجة التسلسُل المُدخل، أي تطبيق عمليّاتٍ حِسابيّة مُعيَّنة عليه، لاستخراج مُوجِّهٍ ذي طُولٍ ثابت يحتوى على خُلاصةِ مُحتوى ومعنى سِلسلة المعلومات المُدخلة، مثلا الجُملة المُدخلة. يُسمَّى هذا المُوجِّه المُستخرَج بمُوجِّه السِّياق. ثُمّ يلتقمُ جُزءُ فَكِّ الترميز مُوجِّه السِّياق هذا بالإضافة إلى عِدَّةِ مُدخلات أخرى، سنستكشِفُها لاحقا، لإنشاء التسلسُل المُخرج كلمةً كلمةً، أي شيئًا فشيئًا بشكل مُتتابع وليس جُملةً في آنٍ واحد.
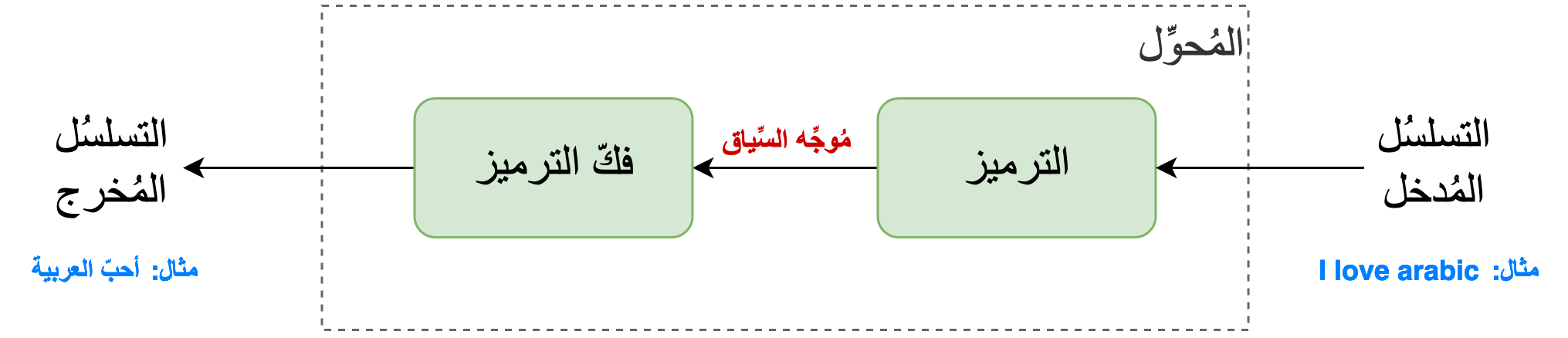
تذكَّر بأَنَّ المُحوِّل هُوَ شَكلٌ من أشكالِ معماريَّاتِ الترميز وفكِّ-الترميز وليس الشكل الوحيد الذي يعتمدُها. حيثُ يتميّز عن غيره من جهة التصميم باعتماده بكثرة على آلية الإنتباه، كما سنرى لاحقًّا. بينما يتميَّزُ من جِهة التطبيق ويشيعُ استعمالُه نظرًا للنتائج الإجابية التي حققها في العديد من مهّمَات مُعالجة اللّغات الطبيعية كالترجمة والتلخيص والإنشاء.
في التَّالي، سنتعمَّقُ شيئًا فشيئًا في تفاصيل مِعماريّة المُحوِّل، ليتحقَّقَ لَديك فهمٌ عميقٌ كافٍ يُمكِّنُك من توظيفها بكفاءة في عملك، و الاستلهام من طريقة تصميمها ومن التمشِّي الذِّي قاد إلي شكلها الحالي في بحثِكَ العِلمي. وسنبدأ رحلة التعلُّم هذه بتفصيل هيكَلَةِ جُزءَي الترميز وفكِّ الترميز المُكوِّنَين لهذه المعماريّة.
هيكلة الترميز وفكّ الترميز في خوارزمية المُحوّل
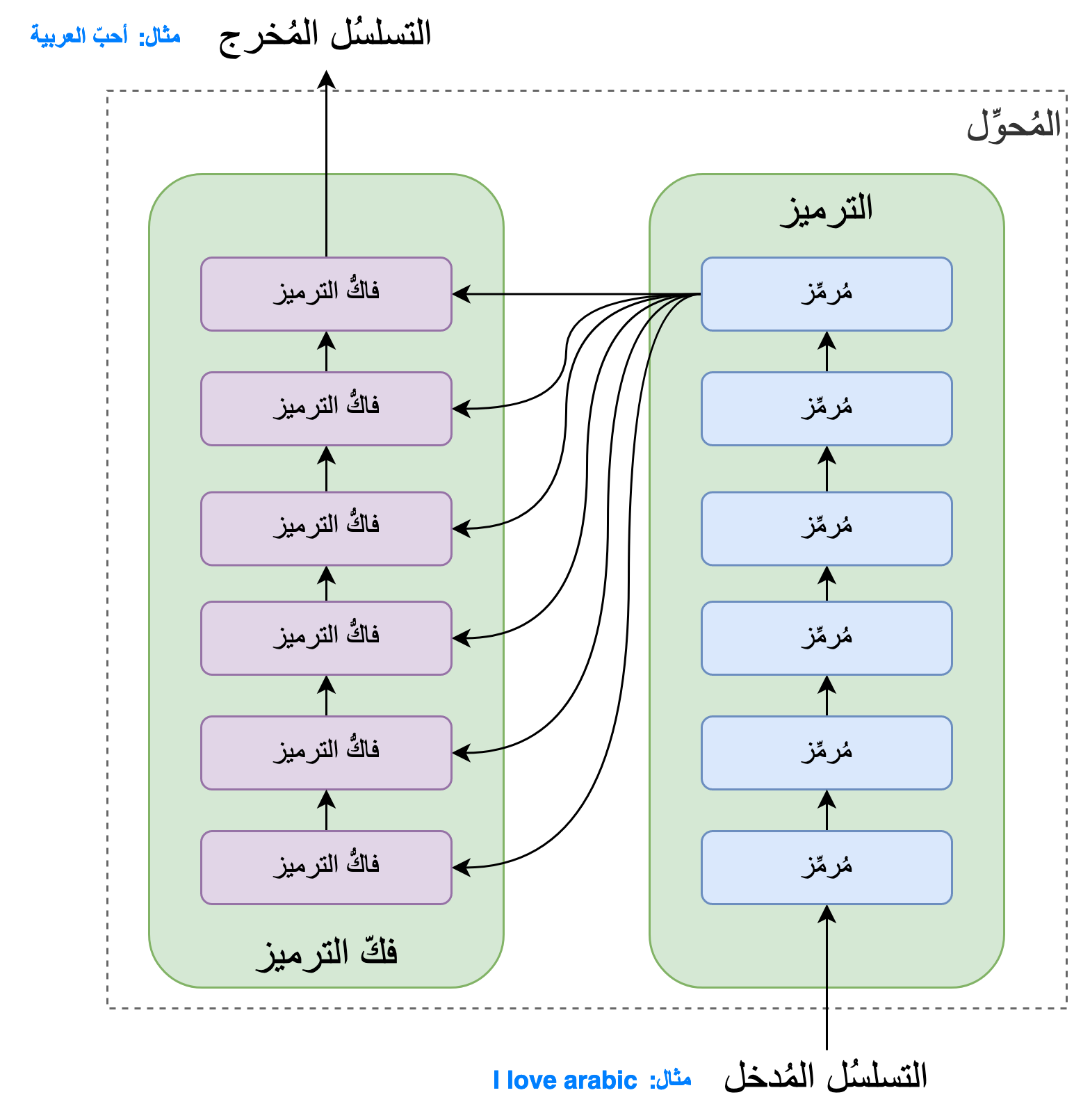
حسب [1] يتكوّن كُلٌّ من شطر الترميز وفكّ الترميز من 6 طبقات، و6 هو اختيار المؤلفين ولك الحرية في تغييره مع الأخذ بعين الاعتبار أنّ زيادة عدد الطبقات تؤدّي إلى زيادة عدد العمليّات الحسابية في النموذج، ممّا يؤثِّر في سُرعةِ وتكلُفة عملِيّتَي التدريب والاستعمال.
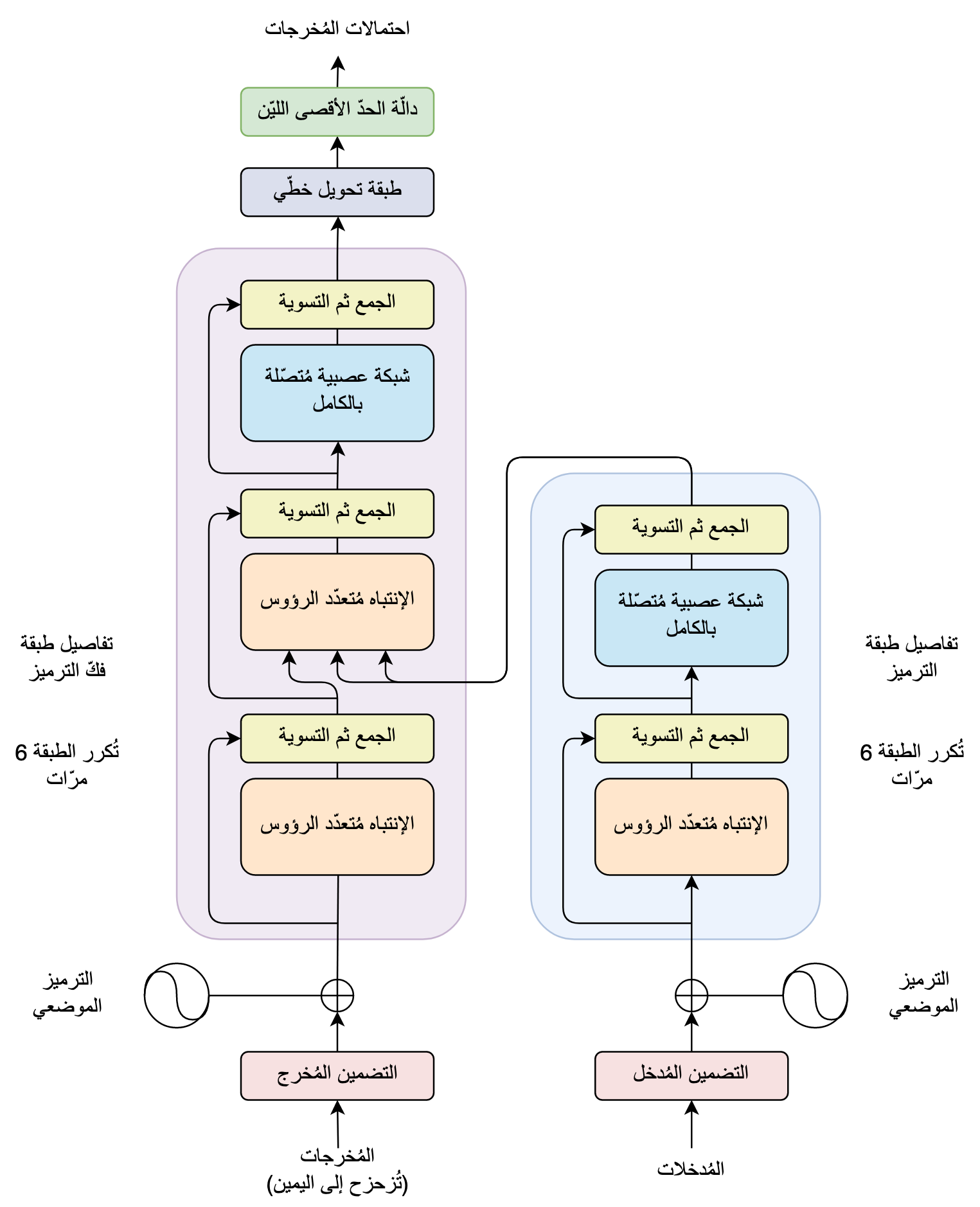
في شطر الترميز، تتكوَّن كُلُّ طبقة من الطبقات الستة من طبقتَين فرعيتَين. الطبقة الفرعية الأولي هي طبقةُ الاِنتباه الذاتي مُتعدّد الرؤوس. والطبقة الفرعية الثانية هي شبكة تغذية أمامية، وهي عبارة عن شبكة عصبية مُتصّلة بالكامل عادية. يُضاف مُدخل كُلِّ طبقة فرعية إلى مُخرجها وذلك ما يُسمَّى بتقنية “وصلة البقية”[3] والتي تُسهِّل عمليّة التحسين لاِيجاد أفضلِ قيمٍ لمُعاملات النموذج. ثم تُطبَّق عمليّة “التسوية”[4] على نتيجة جمع المُدخل مع المُخرج. أنظر في الشطر الأيمن للرسم التفصيلي التّالي لتتوضّح البِنية.
أمّا في شطر فكّ الترميز، تتكوّن كُلُّ طبقة من الطبقات الستة من ثلاث طبقات مُتوالية. الطبقتان الفرعيتان الأولتان هُما طبقتا انتباه ذاتي مُتعدّد الرؤوس. والطبقة الفرعية الثالثة هي طبقة تغذية أماميّة. في هذا الشطر أيضا، يُضاف مُدخل كُل طبقة إلى مُخرجها ثم تُطبّق عمليّة “التسوية”[4] على نتيجة جمع المُدخل مع المُخرج. أنظر في الشطر الأيسر للرسم التفصيلي التّالي لتتوضّح البنية.
الاِنتباه الذاتي مُتعدّد الرؤوس
الفرق بين خوارزمية المُحوِّل ونظائرها من الخوارزمات العاملة على تسلسُلات البيانات هي اِعتمادُها أساسا على آلية الانتباه. فكما تبيّن في الرسم التفصيلي السّابق، تحتوي طبقة الترميز على طبقة اِنتباه مُتعدِّدِ الرؤوس بينما تحتوي طبقة فكِّ الترميز على طبقتَي اِنتباه. ولذا فإن فهم ما تقوم به خوارزمية المُحوّل يحتاج إلى تفصيل لآليّة الانتباه المُستعملة بكثرة داخله.
نرى في الرسم التفصيلي التّالي على اليمين تركيبة طبقة الانتباه الذاتي مُتعدّد الرؤوس، حيثُ يتبين أنّها ترتكز على آلية الانتباه المُعتمد على الجداء السُلَّمِي المُحجَّم. وهذه الآلية ماهي إلاّ سلسلةٌ من العمليّات الرياضيّة المُبيَّنة في الرسم التفصيلي على اليسار.
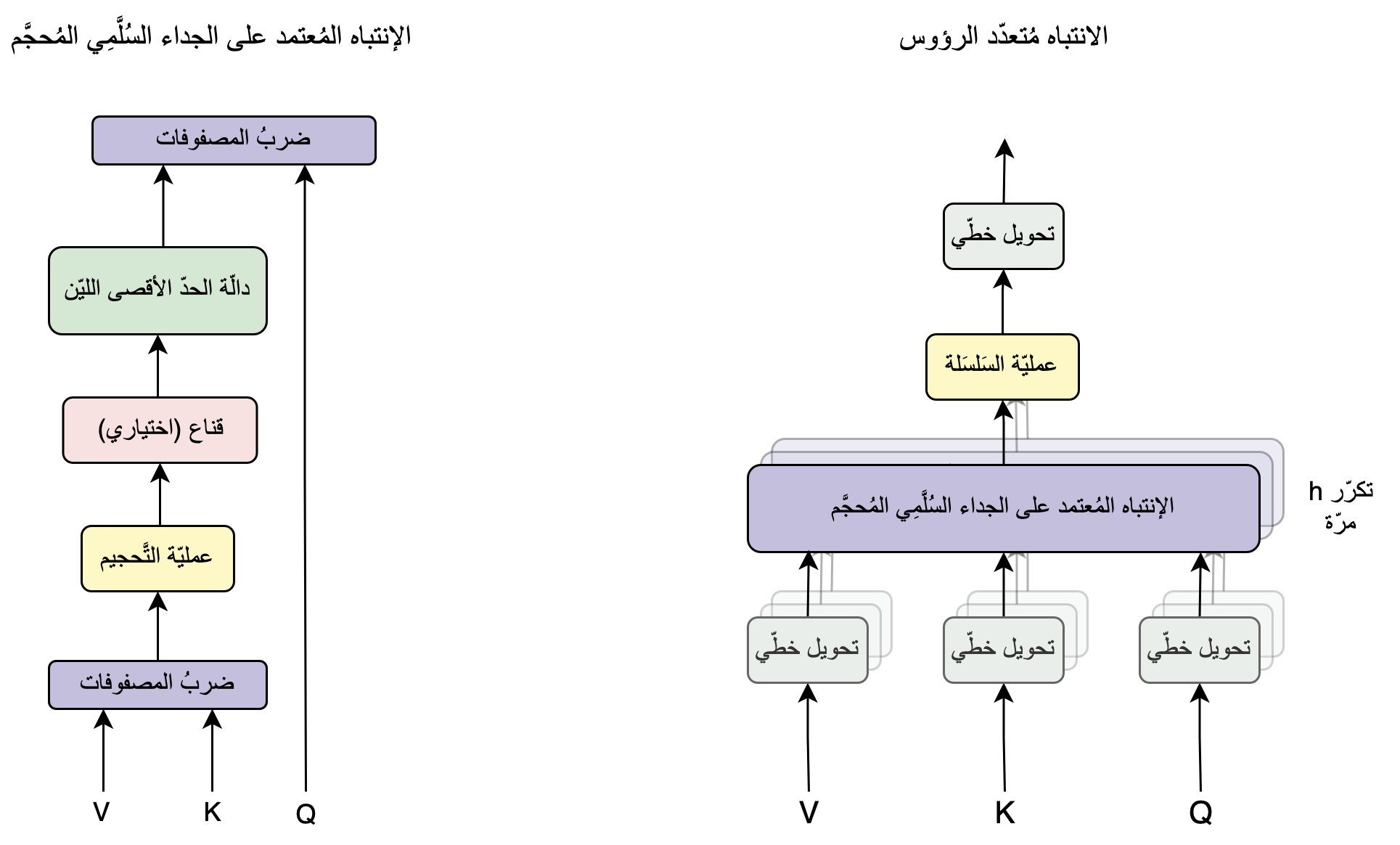
يُمكن اختصار العمليّات الحسابية الحاصلة في آلية الانتباه المُعتمد على الجداء السُلَّمِي المُحجَّم، المُفصّلة في الجانب الأيسر من الرسم التوضيحي السابق، بالمُعادلة الرياضيّة التّالية:
\[Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]في هذه المُعادلة، يُرمز للانتباه باسمه الانجليزي Attention. وهو يقبل ثلاث مُدخلات هي عبارة عن ثلاثة مصفوفات. الأولى Q، وهو الحرف الأوّل من الكلمة Query أي الاستعلام، الثانية K وهو الحرف الأوّل من كلمة Key أي المفتاح، والمصفوفة الثّالثة V من كلمة Value أي القِيَم. سنكتشف لاحقًا مأتى هذه المُسمّيات ومعانيها.
تذكَّر بأنَّ softmax هي كلمة منحوتة من “soft maximum” وهي تعني “الحدّ الأقصى الليّن”. والنحت هو بناء كلمة بتركيب أجزاء مأخوذة من كلمات أخرى، و هي ظاهرة لُغويّة موجودة في عدّة لُغات منها العربية ومثاله قولك “البسملة”.
فهم آليّة الانتباه
حتّى الآن، تعمّقنا في تفاصيل مِعماريّة المُحوِّل حتّى تبيّن الدَّور المركزي لآلية الاِنتباه فيها. لابُدّ الآن من الوقوف على هذه الآلية بعُمقٍ أكبر لفهم تفاصيل عملها وأسباب كفاءتها. فلنبدأ أوّلا باستذكار المُشكل الأساسي الذي صُممت آلية الاِنتباه لحلّه.
ما المُشكل الذي صُمّمت آليّة الاِنتباه لحلّه؟
الإجابة عن هذا السؤال ستُساعد في فهم الأسباب التّي أدّت إلى تصميم آلية الاِنتباه بشكلها الحالي، ولذا فهمها بشكل أعمق. ولتحديد هذا المُشكل علينا العودة بالزمن إلى الفترة قبل اِكتشاف قُدرة آلية الاِنتباه على حلّ مشاكل التعلّم على التسلسلات. حينها، كانت الخوارزمية الأكثر كفاءة في التعلّم على التسلسُلات هي الشبكة العصبيّة التكراريّة والتي تشتهر باسمها المُختصر الRNN، وفيها نوعان هُما LSTM و GRU. يُمكِنك البحث عن تفاصيل نَوعَي الRNN لاحقا، فلن نخوض فيهما هنا لأنّ عدم معرفتهما لا تمنع من فهم تصميم المُحوّل و الانتباه بدقّة.
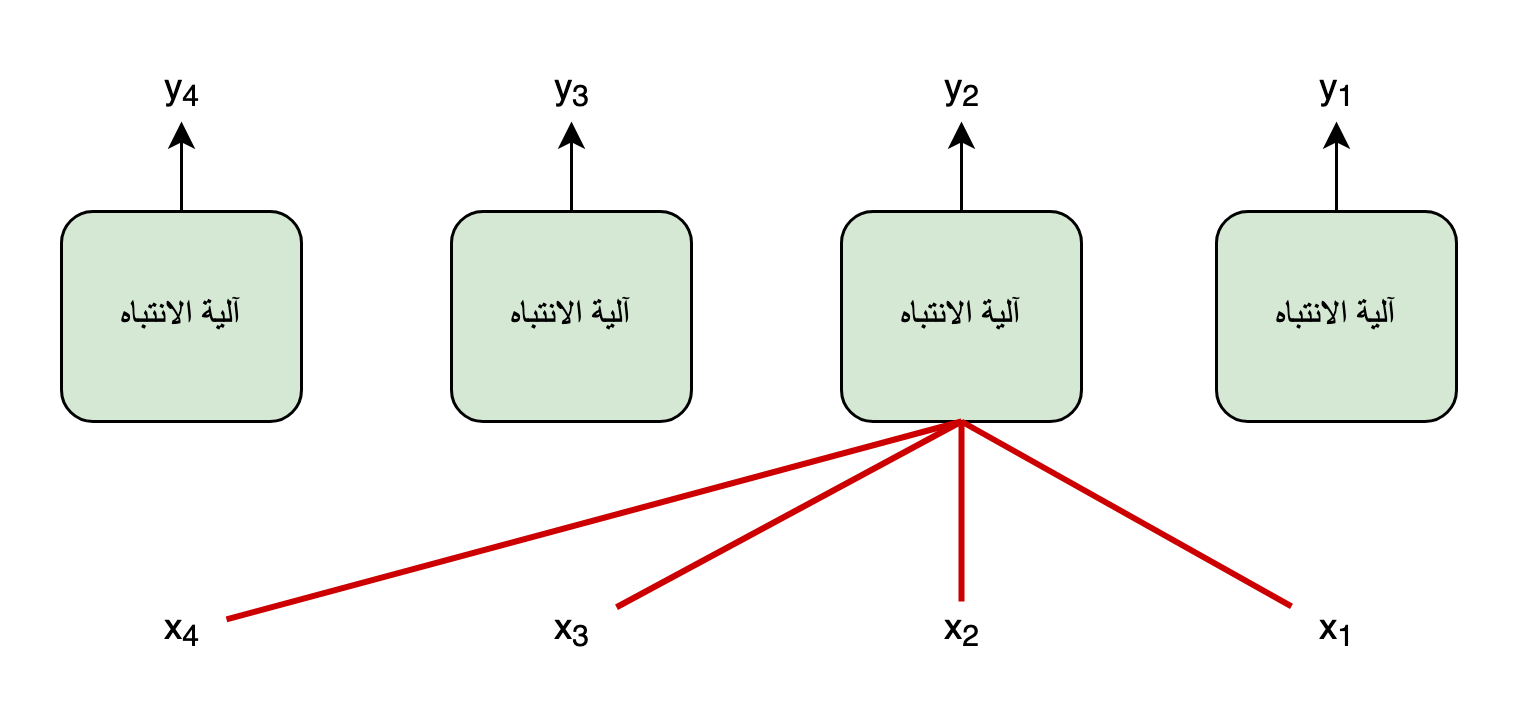
سنكتفي بنظرةٍ عامّة موجزة على الشبكة العصبية التكراريّة حتّى نفهم نقطة ضعفها التّي دفعت إلى اِكتشاف آلية الاِنتباه. لنعتبر أنّ لدينا تسلسُلا مُدخلا، يتكوَّن من عدَّة عناصر، مثلا جُملةٌ تتكوَّنُ من عِدَّة كلمات. لو اعتبرنا عدد العناصر \(m\) و رمزنا ب \(x\) لكُلِّ عُنصر، يُمكننا أن نرمُز للتسلسل ككُل هكذا: \(x_m, ...,x_1\) في الأمثلة التّالية سنتعبر أن \(m\) تساوي 4.
في الرسم التّوضيحي التّالي، تجد بسطًا للمُعالجة التكراريّة الحاصلة في خليّة الشبكة العصبيّة التكراريّة، حيثُ تُظهر الروابط باللّون الأحمر أنّه للقيام بحساب الخليّة في الوقت \(t\) يجب توفير قِيَم المُدخل \(x\) في الوقت الحالي \(x_t\) بالإضافة إلى قيم مُخرج هذه الخلية في الوقت السّابق \(t - 1\). و بما أنّ حساب الخليّة في الوقت السابق \(t - 1\) يحتاج إلى حساب الوقت الذي قبله، نفهم أنّنا نحتاج إلى القيام بالحسابات على كُلّ عناصر تسلسل البيانات السابقة، واحدة تلو الأخرى عبر نفس الخليّة، حتّى نتمكّن من حساب العنصر في الوقت الحالي t. ممّا يعني عدم إمكانيّة حساب كُلّ عناصر المُخرجات \(y_t\) بالتّوازي، لأنّ حساب كُلِّ مُخرج يعتمِدُ على حسابِ المُخرجِ الذِّي قبله.
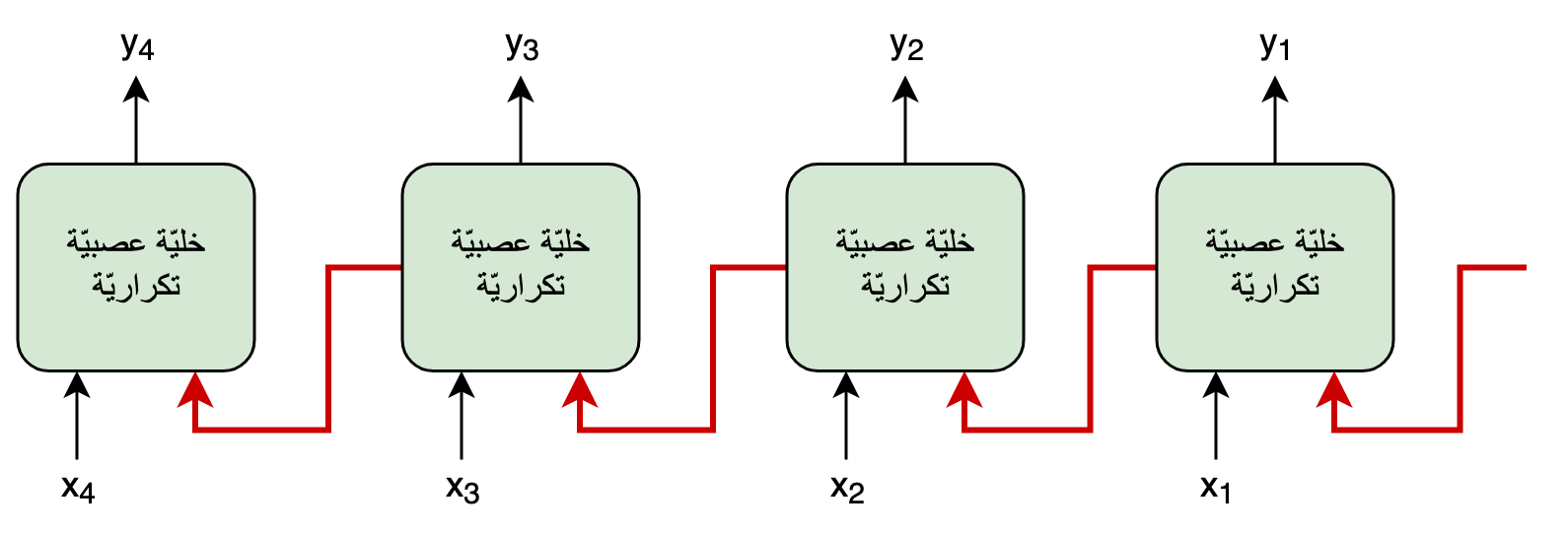
لذا فنقطة الضعف الأساسية في الشبكة العصبيّة التكراريّة هي ناتجة عن هذه الوصلات التكراريّة في تصميمها. فرغم أنّها تُساعد في تمرير المعلومات على طول التسلسُل، إلاّ أنّ وجودها يعني عدم إمكانية استخراج الحسابات في الوقت t من دون القيام بالحسابات في الأوقاتِ السّابقة. وهو ما يحدُّ من سرعة التعلُّم في هذه الخوارزمية، فيؤدِّي إلى بُطئ عمليّة تدريب نماذج الشبكة العصبية التكرارية ككُل.
لذا فهدفُ التصميم الذّي اِنطُلِقَ منه لبلوغ آلية الاِنتباه هُوَ: اِيجادُ طريقةٍ للتعلُّمِ من سلاسلِ البياناتِ بشكلٍ مُتوازي، وليس تسلسُلي أو تكراري، أي اِيجادُ بديلٍ للتعلُّم من دون الوصلات التكراريّة.
الآن، لو نُقارِنُ عمَل الشبكة العصبيّة التكراريّة بعمل الشبكة العصبيّة الترشيحيّة (أو الالتفافيّة)، المشهورة باِسمها المُختصر CNN، نُلاحظ أنّ الأخيرة قادرة على حساب كُلّ المُخرجات بالتوازي اِعتمادً على جُزءٍ من المُدخلات. فهي لا تحتاج إلاّ لمجموعة المُدخلات الموجودة في حيِّز نواة الترشيح حتَّى تقوم بحسابِ المُخرج. وهذا يجعلُ عمليَّة تدريبها أسرع بكثيرٍ من نظيرتها التكراريّة.
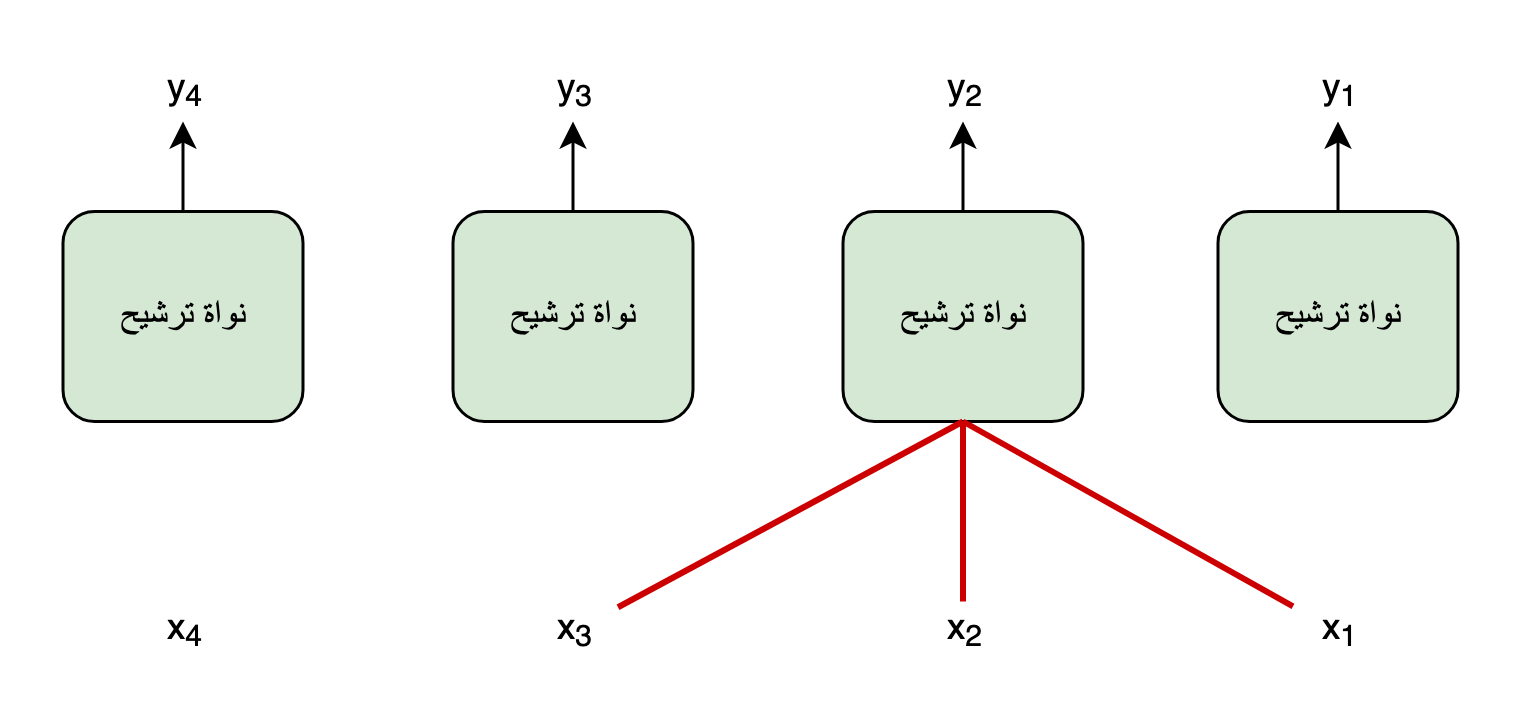
لكن رغم قُدرتها على القيام بالحسابات بالتوازي، فإنّ نُقطَةَ ضعفِ الشبكةِ العصبيّة الترشيحيّة هي محدوديّةُ قُدرَتِها على نمذجةِ الرّوابط بعيدة المدى. ففي طبقةٍ ترشيحيّة واحدة يُمكن للكلمات القريبَةِ من بعضها البعض فقط، بالمُقارنة مع مدى حيِّز عمل النواة، أن تتفاعل فيما بينها. وأمّا إذا أردنا تعلُّم التفاعُلات بعيدة المدى الموجودة في التسلسُل، فيجبُ تكديس عِدَّةِ طبقاتٍ ترشيحية بعضها فوق بعض، وهذا ما يُصعِّبُ اِستعمالها في التعلُّم من سلاسل البيانات طويلة المدى.
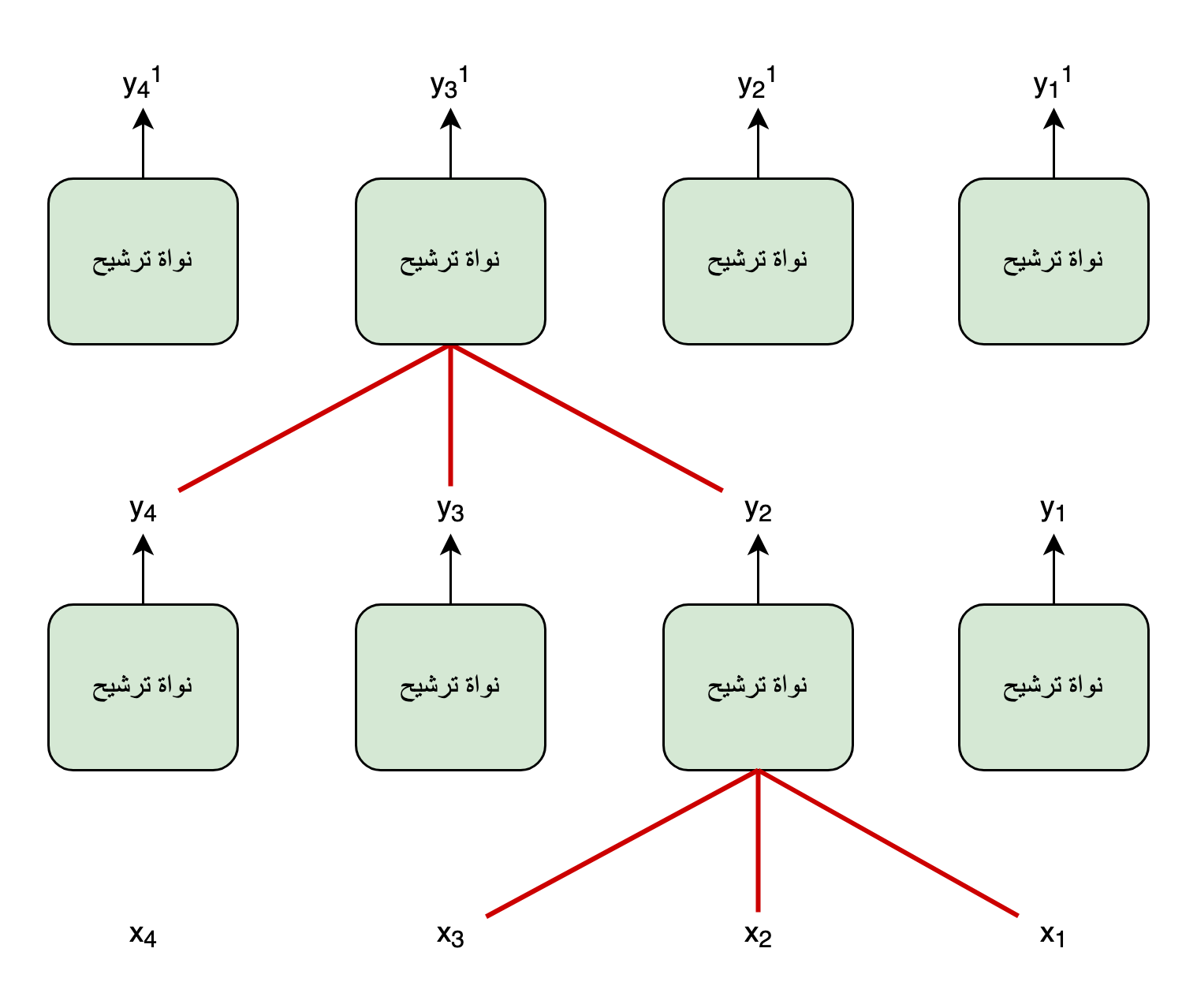
ونظرا لنقطة ضعف الشبكة العصبية الترشيحية في تعلُّم التفاعلات بعيدة المدى من سلاسل البيانات وَجَبَ تحيينُ هدف التصميم الذي قاد إلى استعمال آلية الاِنتباه في المُحوِّل كتّالي:
هدفُ التصميم الذّي اِنطُلِقَ منه لبلوغ آلية الاِنتباه هُوَ: اِيجادُ طريقةٍ للتعلُّمِ من سلاسلِ البياناتِ بشكلٍ مُتوازي، وليس تسلسُلي أو تكراري، أي اِيجادُ بديلٍ للتعلُّم من دون الوصلات التكراريّة مع القُدرة على تعلُّم التفاعُلات بعيدة المدى في سلاسل البيانات
لذا فهدف تصميم خوارزميّة المُحوِّل بآلية الانتباه كان اِغتنام أفضل خواصِّ الخوارزميّات الموجودة حينها دون عيوبها. فهِيَ سعَت إلى نمذجَةِ التّفاعُلات المَوجودة على طُول مدى التسلسُل المُدخل، قريبةً كانت من بعضها أم بعيدة، دون الحاجة إلى اِستعمال الوصلات التكراريّة. ممّا يعني أنّ النموذج الكُلِّي المُعتَمِد على هذه الآلية يُمكن حسابه بالتوازي وبشكل فعّال باِستعمال طريقةِ التغذية الأماميّة.
صياغة آلية الانتباه
لنعتبر أنّ عدد العناصر في التسلسل المُدخل هو \(m\)، ونرمز لكل عنصر ب \(x_i\) حيث \(i\) هو عدد صحيح بين 1 و \(m\) ونرمز إلى مُخرجات آلية الانتباه ب \(c_j\) حيثُ \(j\) هو عدد صحيح بين 1 و \(m\) فأسهل طريقة لحساب \(c_j\) هي باعتبارها جمعًا مُرجّحًا لكُلّ المُدخلات، حيث يكون هناك وزن ترجيح مُعين لكُل مُدخل في الموقع \(i\) مع مُخرج آلية الانتباه في الموقع \(j\) نرمز له ب \(\alpha_{ij}\)، ولذا يُمكن كتابة آلية الانتباه في الموقع \(j\) على النحو التّالي:
\[c_j = \sum_{i=1}^{m} \alpha_{ij} \ x_i\]هذا تمامًا الشكل العام لآلية الانتباه في خوارزميّة المُحوّل كما وردت في [1]، إلاّ أنّ الفكرة الأساسية لآلية الاِنتباه بشكلها هذا قد كانت موجودة قبل خوارزمية المُحوّل، حيثُ انبثقت من احدى الأوراق البحثية المُهمّة في مجال مُعالجة النصوص الطبيعية التي نشرت سنة 2015 تحت عنوان “الترجمة الآلية العصبية من خلال التعلم المشترك للمحاذاة والترجمة”[5]. سنركّز في التّالي على آلية الانتباه كما وردت في خوازمية المُحوّل و لك أن تنظر في [5] إن أردت التعمُّق في الخلفية التّاريخية لآلية الانتباه.
يتبع…
- لتبسيط سُبُل الفهم للقارئ، يعتمد هذا المقال، قدر الإمكان، ترجمةَ المصطلحات التقنية كما وردت في معجم البيانات والذّكاء الاصطناعي الصادر عن الهيئة السعودية للبيانات و الذّكاء الاصطناعي المعروفة بسدايا.
- ترجمة مصطلحات الرياضيّات تعتمد المُعجم الصادر عن مجمع اللغة العربيّة بدمشق.
- هذا المقال للمختصّين، فهو يفترض مجموعة من المعارف المُسبقة عن مجال التعلّم الآلي أو الرياضيّات. إذا أردت القراءة عن مجال الذكاء الاصطناعي لإثراء الثقافة العامة أنظر في مقالات أساسيات الذكاء الاصطناعي.
المُصطلحات التقنية ومُرادفاتُها الإنجليزية
- المُحوّل: transformer
- التسلسُلات: sequences
- التعلُّم من التسلسُل إلى التسلسُل: sequence to sequence learning، و تُختصر ب Seq2seq learning.
- الترميز: encoding
- فكّ الترميز: decoder
- موجّه السِّياق: context vector
- المُرمِّز: encoder
- فاكُّ الترميز: decoder
- دالّة الحدّ الأقصى الليّن: softmax
- طبقة تحويل خطّي: linear transformation layer
- الإنتباه: attention
- الإنتباه مُتعدد الرؤوس: multi-head attention
- التضمين: embedding
- الترميز الموضعي: positional encoding
- التسوية: normalisation
- الإنتباه المُعتمد على الجداء السُلَّمِي المُحجَّم: Scaled Dot-Product Attention
- وصلة البقية: Residual connection
- شبكة عصبيّة تكراريّة: Recurrent neural network
- خليّة عصبيّة تكراريّة: Recurrent neural cell
- شبكة عصبيّة ترشيحيّة: Convolution Neural Network
- نواة ترشيح: Convolution Kernel
المصادر
- الإنتباه هو كُلُّ ما تحتاجه
- التعلُّم من التسلسُل إلى التسلسُل باستعمال الشبكات العصبية
- وصلة البقية
- التسوية
- الترجمة الآلية العصبية من خلال التعلم المشترك للمحاذاة والترجمة
- دليل مصور لشبكة المحولات العصبية: شرح خطوة بخطوة
- شرح المحولات: فهم النموذج الكامن وراء GPT و BERT و T5
- دعونا نبني GPT: البرمجة من البداية وبشرح واضح
- الصورة في رأس المقال من تصوير Robert Linder على موقع Unsplash
